

Custom Search
|
|

|
||
 (2) Moment Area Method. This solution is easier to follow than the
previous method; therefore, it will be described here in detail.
(a) The governing relationship for the motion of a simple
spring-mass system is:
EQUATION:
p - r = ma
(2)
or:
EQUATION:
p/m - r/m = a
(3)
where,
p
=
applied pressure
r
=
resistance of system
m
=
mass of system
a
=
acceleration of system.
Typical load and resistance diagrams are shown in Figure 3.
A plot of p/m
and r/m is shown in Figure 4.
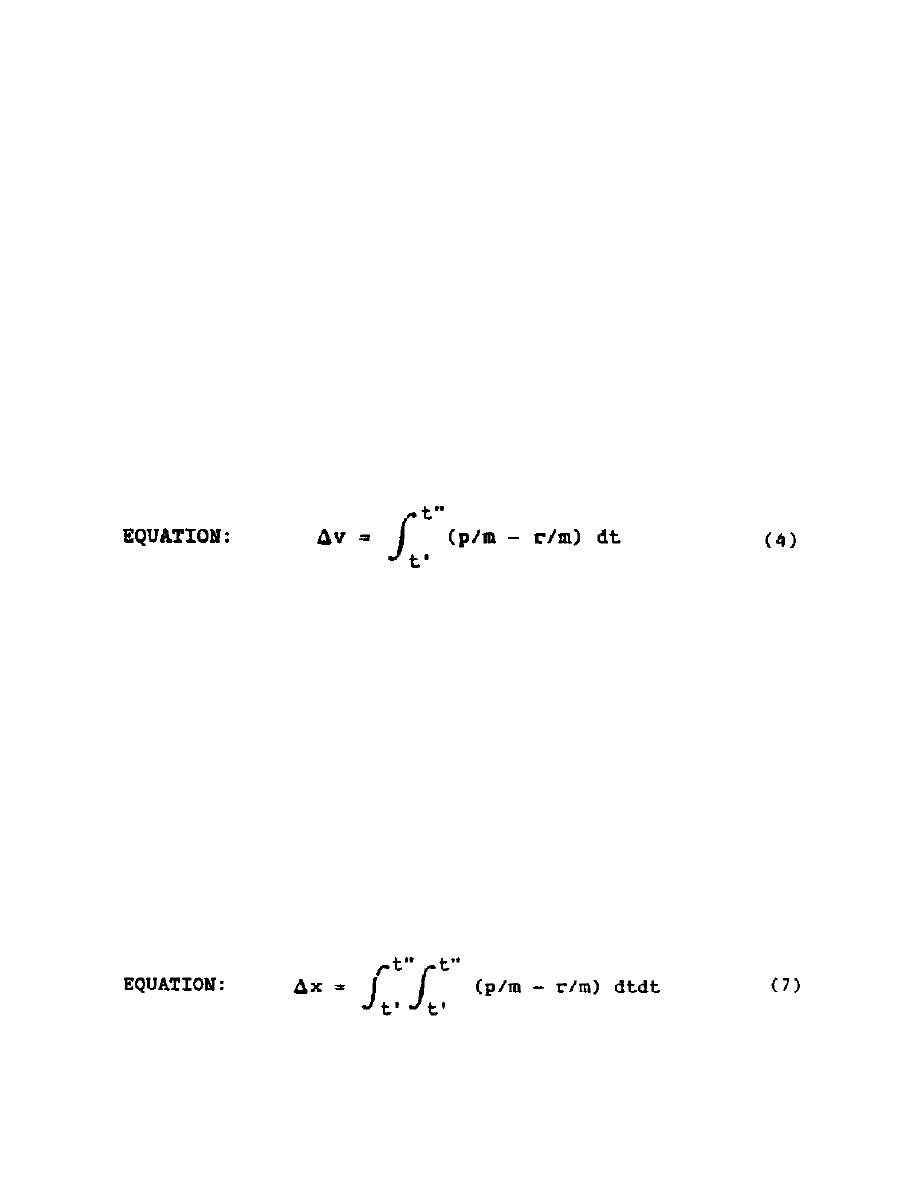
(b) The net area under the curves between time t = t' and t"
is equal to the change in velocity of the mass.
Therefore, the net area under the curves between t = 0 and any t in Figure 4
is equal to the velocity, v, of the mass at t. The velocity is zero at the
time of maximum displacement, tm. Hence, the time to maximum
displacement, tm, is the time in Figure 4 when the net area under the
curve is zero.
EQUATION:
A1 = A2 when t = tm
(5)
If an impulse, i, in combination with the load is applied to the system,
then Equation (5) becomes:
EQUATION:
ib/m + A1 = A2 when t = tm
(6)
The change in displacement of the mass between any time t = t' and t = t"
is:
The net moment of the area under the curves between t = 0 and any time t in
Figure 4 is equal to the displacement, x, of the mass at time t. Therefore,
the maximum displacement of the mass is equal to the net moment of the areas
under the curves about time, tm:
|
 
|
|
 |
||